python 制作CPU压力测试—

众所周知，反正弦函数asin有以下公式（如在计算器中是弧度制下）：

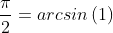
$\frac{\pi}{2}=arcsin\left ( 1 \right )$

百度百科搜索三角函数公式，在泰勒展开式一节中有以下公式：

(doubleFact(2*k-1)/doubleFact(2*k))*(pow(x,2*k+1)/(2*k+1)) — 其中arcsin写错了，(2k+1)!!应该是(2k-1)!!
另外x!!指双阶乘，不同于阶乘

双阶乘实现：

def doubleFact(x):
ans=1
for i in range(1,x+1):
if i%2 == x%2:
ans*=i
return ans

asin函数实现

def asin(x,t):
answer=0
for k in range(0,t+1):
a=(doubleFact(2*k-1)/doubleFact(2*k))*(pow(x,2*k+1)/(2*k+1))
print("k=%d,a=%s"%(k,a))
answer+=a

其中x为角度（弧度），t为计算次数。

注：代码奇慢无比，不要真正用来计算pi，又慢精度又不高，建议只用来编写CPU压力测试程序！

总代吗贴出来：

# import math
def doubleFact(x):
ans=1
for i in range(1,x+1):
if i%2 == x%2:
ans*=i
return ans
def asin(x,t):
answer=0
for k in range(0,t+1):
a=(doubleFact(2*k-1)/doubleFact(2*k))*(pow(x,2*k+1)/(2*k+1))
print("k=%d,a=%s"%(k,a))
answer+=a
return answer
print(asin(1,100)*2)

计算结果：

k=0,a=1.0
k=1,a=0.16666666666666666
k=2,a=0.07500000000000001
k=3,a=0.04464285714285714
k=4,a=0.030381944444444444
k=5,a=0.022372159090909092
k=6,a=0.017352764423076924
k=7,a=0.013964843749999999
k=8,a=0.011551800896139705
k=9,a=0.009761609529194078
k=10,a=0.008390335809616815
k=11,a=0.007312525873598845
k=12,a=0.006447210311889649
k=13,a=0.005740037670841923
k=14,a=0.005153309682319904
k=15,a=0.004660143486915096
k=16,a=0.004240907093679363
k=17,a=0.003880964558837669
k=18,a=0.0035692053938259347
k=19,a=0.0032970595034734844
k=20,a=0.0030578216492580306
k=21,a=0.002846178401108942
k=22,a=0.00265787063820729
k=23,a=0.0024894486782468836
k=24,a=0.002338091892111975
k=25,a=0.0022014739737101384
k=26,a=0.002077661032518167
k=27,a=0.0019650336162772837
k=28,a=0.0018622264064031273
k=29,a=0.0017680811205154183
k=30,a=0.0016816093935831068
k=31,a=0.0016019632753514438
k=32,a=0.0015284115961225677
k=33,a=0.0014603208940791154
k=34,a=0.0013971399176302534
k=35,a=0.0013383869512751784
k=36,a=0.0012836393876290285
k=37,a=0.001232525098500017
k=38,a=0.0011847152561624392
k=39,a=0.0011399183307022236
k=40,a=0.0010978750465914472
k=41,a=0.001058354125872243
k=42,a=0.0010211486797106276
k=43,a=0.0009860731369833312
k=44,a=0.0009529606197429564
k=45,a=0.0009216606921836336
k=46,a=0.0008920374230917098
k=47,a=0.0008639677124658675
k=48,a=0.000837339841602712
k=49,a=0.0008120522129086703
k=50,a=0.0007880122513582057
k=51,a=0.0007651354441371649
k=52,a=0.0007433444987958959
k=53,a=0.0007225686033525614
k=54,a=0.0007027427743614913
k=55,a=0.0006838072810965503
k=56,a=0.0006657071357767537
k=57,a=0.000648391641245871
k=58,a=0.0006318139887619102
k=59,a=0.0006159308995984751
k=60,a=0.0006007023050422869
k=61,a=0.0005860910601175613
k=62,a=0.0005720626870011989
k=63,a=0.0005585851446315293
k=64,a=0.0005456286214729855
k=65,a=0.0005331653487922461
k=66,a=0.0005211694321385132
k=67,a=0.0005096166990104013
k=68,a=0.000498484560941636
k=69,a=0.0004877518884534234
k=70,a=0.000477398897508034
k=71,a=0.000467407046260082
k=72,a=0.00045775894104274026
k=73,a=0.00044843825064875664
k=74,a=0.0004394296280731444
k=75,a=0.00043071863897800795
k=76,a=0.0004222916962219453
k=77,a=0.0004141359998684339
k=78,a=0.0004062394821508707
k=79,a=0.00039859075692766545
k=80,a=0.00039117907320994984
k=81,a=0.0003839942723879085
k=82,a=0.00037702674882018997
k=83,a=0.000370267413484946
k=84,a=0.0003637076604213038
k=85,a=0.0003573393357169886
k=86,a=0.0003511547088217658
k=87,a=0.00034514644598773823
k=88,a=0.00033930758565660254
k=89,a=0.00033363151563102445
k=90,a=0.0003281119518825554
k=91,a=0.00032274291886219894
k=92,a=0.00031751873119201474
k=93,a=0.0003124339766271837
k=94,a=0.00030748350018788655
k=95,a=0.00030266238936928896
k=96,a=0.0002979659603459907
k=97,a=0.0002933897450945759
k=98,a=0.0002889294793644786
k=99,a=0.00028458109143332955
k=100,a=0.0002803406915883404
3.0292687382573695

(责任编辑：IT)

搜索

热门标签:

python 制作CPU压力测试——圆周率计算

双阶乘实现：

asin函数实现

总代吗贴出来：