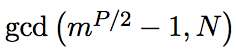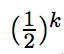|
rsa.jpg
RSA加密 VS 秀尔算法作为RSA加密技术的终结者——“太多运算,无法读取”的秀尔算法(Shor’s algorithm)不是通过暴力破解的方式找到最终密码的,而是利用量子计算的并行性,可以快速分解出公约数,从而打破了RSA算法的基础(即假设我们不能很有效的分解一个已知的整数)。同时,秀尔算法展示了因数分解这问题在量子计算机上可以很有效率的解决,所以一个足够大的量子计算机可以破解RSA。
然而,有一种技术可以让RSA加密无用武之地。秀尔算法可以破解RSA,但是怎样才能让它真正见效呢? 我们这里并非建议你同时尝试所有可能的质因子。 而是使用(相对)简洁的语句: 如果我们快速找到下面这个周期函数的周期, f(x) = m^x (mod N) 我们便可以破解RSA加密。 秀尔五步走那么,秀尔算法究竟是怎样工作的呢?在秀尔五步法中,只有一步需要是需要用到量子计算机的,其他的步骤则都可以采用传统方法解决。 第一步:使用传统最大公约数分解(gcd)算法,也就是辗转相除法。N是你需要尝试的因子,m则是一个小于N的随机正整数。 如果gcd(m,N)=1,则继续。一旦你使用gcd找到一个因子,你便能获得一个非凡因子,然后结束。 第二步:找到周期 P m mod N, m^2 mod N, m^3 mod N 这是使用量子计算的一步。 第三步:如果周期P是奇数,回到第一步,选择另一个随机整数。如果不是,继续下一步。 第四步:检验
如果成立,则继续第五步;反之,回到第一步。 第五步:解
解得一个非凡素因数N的值,然后你便能破解RSA加密了。 第二步是怎样实现的?然而,量子计算机是如何找到函数周期的?这又为什么如此重要? 我们来看一下周期 P : m mod N, m^2 mod N, m^3 mod N (由于这是一个指数函数,我们可以将一个复杂的质数转换成双曲正弦、余弦然后得到周期) 这个发现周期的过程需要依赖量子计算机同时计算许多状态的能力,也就是状态的“叠加”,因此我们能找到方程的周期。 我们需要这么做:
与传统情况类似,在这些转化之后,一个测量值将会产生一个近似方程周期的值(你可以获得“波峰”,就像傅立叶变换中的,而准确性会更高一点)。使用量子傅立叶变换,我们能够解决排序和因数问题,这二者相同。量子傅立叶变换可以让一台量子计算机进行相位估计(酉算子特征值的近似值)。 当你完成量子部分(第二步)的时候,你可以检查一下周期的有效性,然后使用另一个传统的最大公约数算法得到密钥的质因素。 有趣的是,由于这项技术并不是在于找到所有潜在质因数,而是找到潜在周期,你就不必尝试很多随机数直到找到一个成功的质因数N。如果P是奇数,那你不得不回到第一步,这里
K是一个不同于N的质因素。因此,即使你加倍密钥长度(N),寻找质因数也不会出现放缓的情况。RSA是不安全的,同样加倍密钥长度也不能帮你抵御量子计算的汹涌来袭,而保障安全。
量子傅立叶变换被用于建立量子线路,使得秀尔算法的物理实现成了量子计算机最为轻松的任务之一。 量子傅立叶变换:青出于蓝
量子傅立叶变换是许多量子算法的关键所在。它并不加速寻找传统傅立叶转变,但是能够在一个量子振幅内执行一个傅立叶变换。在一台量子计算机上可以指数增长般快速处理量子傅立叶变换。虽然超过了直接映射经典傅立叶变换的范畴,量子计算机也可以做其他的事。例如,解决隐子群问题(也就是解决离散对数问题),或是计数问题(解决了这个问题就可以解决现代密码学中很多其他形式的密码)。更重要的是,量子傅立叶变换可以应用到机器学习、化学、材料科学或者模拟量子系统。 秀尔算法中只有一个步骤是需要在量子计算机上完成的,其他的都可以在普通的超级计算机上完成。量子计算机运行完子程序后就会将结果返回给超级计算机让它继续完成计算过程。量子计算机可能永远不会是单独存在的,而是一直和超级计算机配合执行任务,经过这样的配合它们就可以破解RSA密钥。 因为篇幅有限,很多数学细节和证明过程就不再赘述了,如果你对这些数学解释感兴趣,如果你具备线性代数、群论、高等数学的知识,你可以看看这些: *参考来源:medium,vulture对本文有贡献, (责任编辑:IT) |